Welcome home, sir

I have to say that the one thing I really envy to the Americans is the way they are greeted by homeland security when they go through passport control in any US airport. In Italy, they barely look you in the eye, even less so if you are an Italian person showing your passport (which Italians usually don't, since most of them use their ID $-$ or carta di identità $-$ when they travel abroad).


Nevertheless, I was given a real "welcome home, sir" by Trenitalia. When you buy a ticket, you automatically reserve a seat (which you pay for). You'd think that this guarantees you have a seat on the train, but because they actually let twice as many people in, this is not always the case. 


I got on the train in Bologna only to find some people occupying the seat I have reserved. Here's my reaction. They insisted I checked their ticket to argue their case, which I did. They were indeed in the correct seat, but on the wrong train (they should have been on the next one). I suggested that this may have been the problem, but they weren't impressed by my logic $-$ silly me! So I decided to give up since it was too hot to start an argument (which surprises me: I must have really grown up!) and evidently I'm not used to the heat any more. I pretended that I was wrong and went to stand up in the corridor. Luckily, the train only takes 35 minutes to get to Florence, so that wasn't too bad.

τὰ Ὀλύμπια

Due to my very limited photographic skills (OK, as usual I digress: it's not so much a problem of limited skills $-$ well, a bit of that too $-$ my main problem with taking pictures is that I'm too impatient and I easily get bored. For some reason, taking pictures is one of the activities that bores me most), it's probably not very easy to see from the picture here.


But: finally, the tickets for the Olympics have arrived. Off the top of my head, I have a few considerations.

1. I forgot that I actually bought 4, so I have 2 spare, I think.
2. I didn't expect to have a free travel card to use public transport for that day. That's kind of nice.
3. Again, you probably can't see it (unless you zoom the picture so much that the resolution is too low), but it's kind of cool that they have printed the name of the person who bought the tickets on the actual thing. Right below the "L" of the London 2012 logo, or just above and slightly to the left of the Olympic circles, there's a very small bit with my name on it. That makes me feel soooo special!

The event that I "won" is volleyball. It's the day after I'm back from San Diego, so the games better be good or else I'll fall asleep on TV!

When the going gets tough...

Getting closer to my personal Euro2012 derby: England v Italy. 


I find amusing that both sets of media think that their respective team have been gifted a good tie. The English are very happy to have avoided Spain, while the Italians don't mind not playing the French. I guess these both make sense (particularly for the Italians, it is always very tense when we play France and I suppose we do mind the thought of getting kicked out by them).


But: may be there's something quite not adding up when both sides think they are favorite and that it is their turn to shine and go through to the semis. I really think it's a very close game and my subjective prior for the game is genuinely vague. Here's how I would proceed to formalise it.


First I would look for "hard" evidence to inform my thought process: Italy have played England 23 times; we have won more games (9 to 7) but overall have a worse goal difference (26 for and 28 against). In the last 15 years, we've played each other only 5 times. In the two official games Italy won one (at Wembley) and drew one. Italy also won two of the friendly games, while England won the remaining one. The last of those occasions was in 2002 and Buffon is the only player to still be around (as an active footballer, that is). So, I think all in all these stats are not very helpful to inform a prior distribution. 


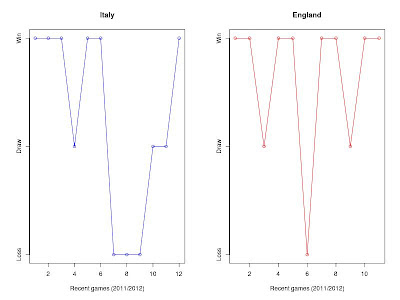
Then I would look for info on more recent games, even if not head-to-head. The graph below shows the recent form of the two teams (in every game they played in 2011/2012, including the first games in the Euro2012).

Looks like England are doing a bit better of late. However, the last three (competing) games were against: 

1. a very good opponent (Spain and France for Italy and England, respectively); 
2. a good and a so-so opponent (Croatia and Sweden); and 
3. a so-so and a good opponent (Ireland and Ukraine). 

So, the difference in form seems to be in the fact that all other things equal (well, not really, but you know what I mean...) England managed to get a scruffy win aganist Ukraine, while Italy failed to hold on long enough and conceded an equaliser to Croatia. On the other hand, England have not succeeded in winning 3 games in a row in the last year. Again, probably not too much to go about to distinguish among the teams. 


So, one way to form a prior is the following. Assume that I'm willing to consider a convenient parametric distribution for $\theta$, the probability that Italy win the game. For example, I can consider $\theta \sim \mbox{Beta}(\alpha,\beta)$.  [As usual, this is just one of the possible forms for the prior; there's nothing special about it, if not its mathematical properties!]


Now, consider these three quantities:

• the (assumed, by me) mode of the distribution. Given all the uncertainty, which I was not able to resolve by looking at existing data, I'll assume this to be 0.5, meaning that I am really very uncertain about who's going to win and think that the best bet is 50:50.
• The (assumed, by me) upper level of probability that I can consider as reasonable to represent the chance that Italy win the game. Of course, I don't think that there is absolute certainty that Italy will go through, so this level will be less than 1. I think I would go as far as to $u=$.8.
• The (assumed, by me) cumulative probability that $\theta<u$. This gives an indication of the uncertainty that I'm placing over this distribution, while imposing some mathematical constraints on it. For example, because I'm assuming that $u=$.8 and that mode$=$0.5, this cumulative probability should be relatively large. I feel confident that this would be a reasonable upper limit, and thus I consider $p=\Pr(\theta<u)=$0.85.

With these values and using some reasonably simple code (optimising the values of the parameters $\alpha,\beta$ to meet the constraints just imposed $-$ discussed here), I can derive that my choice is equivalent to considering $\alpha=\beta=$3.2618. This is my resulting prior.

Not very informative $-$ in fact almost at all. I'm saying that in my view, before the game starts and having observed the relevant evidence available to me up to now, my assessment of the probability that Italy beat England is somewhere in between 15% and 85%. Still, just a bit better than a standard "minimally informative" prior, eg Beta(0.5,0.5). More importantly, it forces you (or me, in this case) to think of the consequences of the choice in terms of the probabilities that are induced by this choice.

Estimating the predictive distribution of the result is the actual objective of the exercise. In fact, I'm not really interested in $\theta$. Given this (prior) information, a large number of simulations produces a median value of 1, which means that I'm predicting Italy to win $-$ but with a huge uncertainty attached.

Bayesian hierarchical glaucoma

Last year (in fact I did some of this while travelling to go to my friend Lorenzo's stag do $-$ he's the one in white, but with no veil), I worked on a clinical paper discussing the prevalence of glaucoma with specific focus on the European population. The objective was relatively straightforward, except for the fact that the studies used to derive the estimations were quite heterogeneous and thus we could not pool them altogether.


So we used a nice (I think) Bayesian hierarchical model where different studies contributed to different parts of the estimation procedure. I built a model in which the overall prevalence was estimated using separate (but connected) modules $-$ basically age groups. So we first estimate a set of "level-1" parameters $\theta_1,\theta_2,\theta_3,\theta_4$ (effectively the age-group specific prevalences) using the observed data from the available studies. Some of these are assumed to be conditionally exchangeable, so that for example $\theta_2,\theta_3,\theta_4$ are used to inform the distribution of the parameter $\theta_5$, representing the prevalence among the over 50s. Again assuming conditionally exchangeability, $\theta_1$ and $\theta_5$ are used to inform the overall prevalence among the over 40s.

We have found sensible (or so I'm told by the clinicians!) results. It wasn't the place to brag about the use of a Bayesian approach, so the paper does not give much detail on the actual model. The observed data were counts of subjects with glaucoma in the study populations.


But it was cool that I persuaded them to report the results in graphical fashion and with the credible intervals.

Some of them do not even know that the model is Bayesian, but they were extremely happy with the results (or if they weren't, they were extremely nice to me anyway). 


The paper is out now.

Biscuit

Vinnie the Panda (kind of a New York style wise guy, who advertise a brand of biscuits talking like my cousin Vinny) says: "These guys know a thing or two about biscuit!".


I think it's only fitting that the Italian media are now all over the fact that if Spain and Croatia (more or less explicitly) agree on a 2-2 draw Italy are out of the Euros no matter what. They call it a "biscuit". After all, we do know a thing or two about biscuit, given all the match fixing, professional footballers betting on games they were playing in and so on. 


I can see Spain doing their usual game with over 85% possession and eventually breaking the Croatians so that even a miserable 1-0 at the 96th minute will see us going through. I think it's a bit less likely that they actually draw 2-2, but I'm afraid it's also quite not a given that we'll beat the Irish. 


Having said all that, I really do not care that much about how it'll go tonight. Honest!

Storm after the storm

Veeeery slowly but reasonably surely, I'm working my way up the pile of unfinished things that I have miserably neglected in the last month or so. 


I think I've just closed the telomere paper and I'm almost ready to work on the Eurovision contest paper (we've run the final model, so I should be able to write some stuff up so we can send it out $-$ this time we're aiming high; let's see how it goes!). 


A couple more prescriptive things (ie work that I don't particularly care about, but that I have to do, given that it is paying at least part of my salary); the next bit of the HPV model (in which we are starting to include sexual mixing $-$ sounds kinky, but it just means allowing the poor simulated cohort to have sex); and a couple of nice summer projects I'm supervising (I'll post more on these when I have a bit more time).

Then I should be ready for a short, but much needed break. First, we'll go here

and then, we'll spend a few days here

(hopefully with weather just like in the pictures!)

The next Harry Potter?

The editor just sent me the cover of the book. I think it looks pretty cool (but I would say that, wouldn't I?...).

I think it will be released later this year (probably September/October). More info (including a table of contents) here; I'll put the codes for some of the examples and other stuff on the website as well. 

Of grants and grunts

I'm about to finish writing up the proposal of a research grant I'm applying for. It's about the use of Regression Discontinuity Design to evaluate interventions in primary care. 


The idea is quite clever, I believe: say that there is a clear rule to guide the way in which patients are (or aren't) given a treatment, and this rule is associated with a continuous variable. For example, say that you are given drug $d$ if your blood pressure is above some level $x$, but you are not if it is below. If this is reasonable, subjects just on either side of the threshold can, to some degree of approximation, be considered as randomly allocated to the treatment, thus mimicking controlled conditions.


Of course, this doesn't necessarily eliminate bias and confounding, but it goes quite some ways in limiting the impact of these problems. Also, it turns out that in clinical practice there are quite a few examples of situations that fit this framework. So we're proposing all sorts of cool investigations $-$ hopefully they'll like it and give us all the money we've asked, which I'll then use to buy new players for newly promoted Sampdoria.


That's for the grants part. 


Grunts are about: 

1. the fact that I'm really getting fed up with reviewing the proposal and I'm really looking forward to the moment I'll submit it; 
2. the fact that the waitress misplaced our pizza order, which means it took her forever to bring our food;
3. English summer rain (which at the moment seems to have stopped, but the guy on BBC has just said there's more to come).

Euro 2012 predictions

In the run up to major football events, the guys at the Norwegian Computing Centre always prepare their predictions for the final results. They use a relatively simple model which predicts the number of goals scored by team $t_1$ when playing team $t_2$ as a function of a "baseline" scoring intensity, corrected for the relative difference in strength between the two teams.


This is not too dissimilar from the method that Marta and I used a while ago (by the way: interesting story. I was trying to have an excuse to bring more football into the household $-$ she got interested in the model, but no actual increase in the time spent watching games has ever been recorded). 


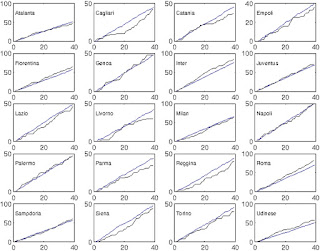
Our main point was that there is indeed correlation between the number of goals scored by the two competing teams, but instead of using complex forms for the likelihood (eg bivariate Poisson models), it can all be accounted for by extending the structure to a hierarchical model, based on independent Poissons that are connected through common structured effects. We did reasonably well:

(the black line is the observed dynamics in terms of points through the 2007-2008 season of the Italian Serie A, while the blue line is our prediction; for most teams the prediction is really good).


In our case, we were estimating results from national leagues, which I think is a bit easier, given that there are more data and that the seasons are longer, meaning that the "true" values tend to come up with a stronger signal (and stronger teams will be predicted to score more goals and thus win more games). There was an interesting issue with overshrinkage (check the model out).


In the case of international tournaments, prediction is a bit more complex; the tournament is played over just a month and there is much more scope for random variability in the performances of the teams. Thus, all in all, I think that their model is OK and will probably do well in terms of prediction. The nice feature is that they will update the predictions as more games are played (not sure they do it in a proper Bayesian fashion $-$ not saying they don't; just haven't read the details).


The predicted semi-finals are Spain-Germany and Italy-Netherlands. I think we'd be happy to reach the semis. We may have a shot, but I wouldn't be too surprised if we went back home much sooner (but that's me being a bit pessimistic, may be).

Norway

I vaguely knew about Norway, but having being there for a few days I could actually see and ask a few things about it. It's amazing and humbling how they managed to make the country work. The fact that they have invested 20 years on learning how to work with oil and gas (which is now paying off amazingly, with their sovereign wealth fund) is really a lesson that should be learnt by so many politicians (and voters!) around the world.


Surely it is much easier to run a country of 6million people than one that is 10 or 50 times as big, but still their welfare state is impressive.


On the other hand, the cost of living is ridiculously high: the equivalent of £5.03 for a coffee (check this out! $-$ as of just now, Google currency converter says £0.107 for 1 Norwegian Krone) really is steep. 


Anyway, very interesting place $-$ to visit.