BCEA 2.0

I know that updating a package too often is not quite good practice, so, given we've released BCEA 1.3-1 just about a month ago, this is way too soon to move forward. But between the last release and now, I've been doing some reading and have made some major changes to the function that computes the expected value of partial information (EVPPI) $-$ more on this here. In fact, the changes are so major, that I've decided to move BCEA to release 2.0, which I'll upload on CRAN in the next couple of days.

The new version implements two quick and general methods to compute the EVPPI. These are both "univariate" methods, in the sense that you can compute the separate impact of each parameter in a model on the overall expected value of information. This is not necessarily ideal, because there might be (and in general there is) posterior correlation among the model parameters and thus it would be optimal to consider that in computing the EVPPI. 

Of course, one can always perform multivariate EVPPI analysis using the 2-stage MCMC approach (described in BMHE) $-$ but that is very much likely to be computationally intensive. Apparently, a new version of Strong and Oakley's paper is under preparation to deal with multivariate EVPPIs.

Here's an example of how to use the new code, from R $-$ when I've actually uploaded it, that is...

library(BCEA)
data(Vaccine)
ls()
   [1] "c"             "cost.GP"       "cost.hosp"     "cost.otc"  
   [5] "cost.time.off" "cost.time.vac" "cost.travel"   "cost.trt1"
   [9] "cost.trt2"     "cost.vac"      "e"             "MCMCvaccine" 
  [13] "N"             "N.outcomes"    "N.resources"   "QALYs.adv" 
  [17] "QALYs.death"   "QALYs.hosp"    "QALYs.inf"     "QALYs.pne" 
  [21] "treats"       

m <- bcea(e,c,ref=2,interventions=treats)

input <- CreateInputs(MCMCvaccine)
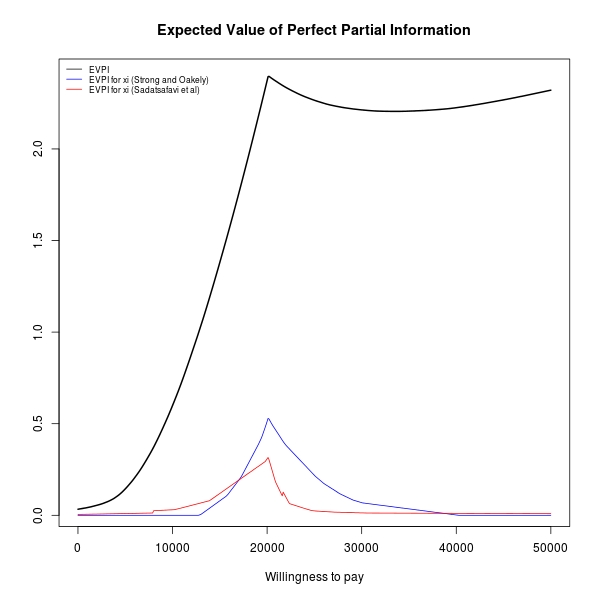
x.so <- evppi("xi",input$mat,m,n.blocks=20)   # Strong & Oakley method
x.sal <- evppi("xi",input$mat,m,n.seps=2)     # Sadatsafavi et al method

Of course, you load the package and then the dataset which comes with it. It includes the variables needed to run the health economic analysis, which is done by calling the function bcea. So far, nothing new (as far as BCEA is concerned).

The new bits involves a call to the function CreateInputs, which takes as input an object in the class rjags or bugs; this is basically the result of the MCMC model that produces the posterior simulations for the variables of interest (in the current case, that's essentially e and c). The output of CreateInputs is a list including the string vector of available parameters that can be used for the EVPPI analysis and a matrix with the simulations for all of them (each column is a parameter).

Finally, you can compute the EVPPI for one or more parameters calling the function evppi (note that the first argument of the function can be a vector including more than one parameter; in this case, the univariate analysis will be repeated for each of them separately). The other arguments are the matrix of simulations, the BCEA object including the basic health economic analysis for the current model and a specification of the method chosen.

The results can be visualised using the specific method plot for the class evppi and show the overall EVPI with the EVPPI for the selected parameter(s).

The two methods (neither of which estimates the EVPPI without bias, although they are proved to do a good job!) generally agree $-$ although there is some fiddling to do with their parameters (for example the number of blocks in which the matrix of parameters simulations and utilities is decomposed in Strong & Oakley's method).

JSM 2013

Next week I'll head to the Joint Statistical Meeting (the annual conference of the American Statistical Association), which funnily enough this year will be held in beautiful Montreal, Canada.

I've been once to Montreal for a couple of days and, despite the fact it was very, very cold (something like 3-4 degrees, despite the fact it was mid May!), we loved it. 

I'll give a talk on the Regression Discontinuity Design in a very interesting session organised by Fabrizia Mealli. Not for the first time this year, I'm doing reasonably well with preparing the slides (not finished yet, but getting there)...

Today I've flipped through the programme and it looks as though there are quite a few very interesting sessions. In fact, the programme looks more interesting than the one last year $-$ it wasn't too bad, but the few talks I really wanted to see where always clashing. For this year, there is only a (massive) clash on Tuesday afternoon, with a session on spatial stats (featuring Håvard), a session on causal inference (including Guido Imbens) and Judea Pearl's masterclass on the mathematics of causality all scheduled at the same time! I'm sure that organising the timetable for such a big event must be a nightmare, but this is just unfortunate...

Mugatu is a health economist

When Hansel comes out to save the day preventing "Derek [Zoolander] to off the prime minister of Micronesia", the evil Jacobim Mugatu says "It's that damn Hansel – He's so hot right now!".

Quite in a similar fashion(?), it seems as though in the last few weeks the Expected Value of Partial Perfect Information (EVPPI) has become so hot...

First there was Mohsen Sadatsafavi's paper (which I have mentioned here and whose method I've already implemented in BCEA). Then, the Bristol workshop (on which I reported here). And then, just last week, another quite interesting paper (by Mark Strong and Jeremy Oakley) has appeared in Medical Decision Making, discussing pretty much the same issue.

The problem is, in theory, relatively simple: given a bunch of parameters subjected to uncertainty, we want to compute the value of reducing this uncertainty on one (or some) of them, eg by collecting additional information. In health economic evaluation this is particularly important, as the current decision may be (and in general is) affected by how well we "know" the value of the model parameters. Thus, the decision-maker may be in the position of being better off by not making a decision right now and deferring until someone (for example the pharmaceutical company trying to market some new drug) can come up with some extra information $-$ incidentally, these concepts could be used to negotiate co-payments, as we argue here.

From the computational point of view, the calculation of the EVPPI can be dealt with using 2-stage MCMC simulations, which can be quite demanding. Thus, people are trying to research clever methods to reduce the computational burden.

I think these are all very interesting, especially because, unlike the 2-stage MCMC approach, these methods seem very general and thus can be applied to, virtually, any model, especially when it's run under a Bayesian framework (eg like I do in BMHE). I'll try to talk to Strong & Oakley and possibly implement their method in BCEA too!

BCEs0

BCEs0 is the new R package I've written $-$ well, nearly finished to, anyway; it should be ready in version 1.0 in the next few days. The acronym stands for Bayesian models for Cost-Effectiveness with structural 0s, and it basically implements the model I briefly (and probably a bit confusingly) described in a previous post, here. 

I've submitted the full paper (in which I present the whole model in much more details) to arxiv $-$ that's the first paper I've put there. It should be available from Tuesday. Also, I created a webpage in which I've put some explanation. I'll include all the relevant links and documentation there, soon.

On a related note, I have struggled a bit to create the webpage because I wanted to include some of the maths notation (using LaTeX fonts). But of course, Google sites, which is otherwise quite OK, I think, wouldn't allow me to do that. So, I've reverted to using Texify, which allows you to create LaTeX symbols and then include them (sort of OK) in the html code (here is a nice guide $-$ of course Google Docs doesn't exist any more, but Drive can be used instead).

Interview

Apparently, while at the next JSM in Montreal (in which I'll present some work on the RDD project $-$ of course, the talk is still far from being written, but scheduled for next week), I'll give a video interview to promote the book. 

The brilliant people at CRC asked me if I was up for it. I am, although I have to say I'm feeling a bit nervous about it. The idea is at the same time extremely embarrassing and exciting $-$ I'm hoping the excitement will trump embarrassment. I think the video will be posted on YouTube.

But, then again, come to think about it, I do have plenty of experience in televised interviews, like this (again, rather embarrassing) clip shows...

Zero to hero

Recently, I've been working on a paper, which I think is coming along nicely. The basic problem is like this: in a health economic evaluation, sometimes data are collected on a sample of individuals. Say, for example, that $n_0$ subjects are given a standard treatment $t=0$ and $n_1$ are treated with a new intervention $t=1$. For each subject, we typically observe a measure of clinical benefit $e_i$, which tells us how "good" the treatments are, and a measure of overall cost $c_i$. 

Costs (and for that matters benefits) are almost invariably associated with skewed distributions (and thus suitable models are Gamma and log-Normal) and, generally $(e,c)$ are actually correlated. Moreover, sometimes, for some of the patients, $c_i=0$, ie some people are observed to accrue no costs to the NHS. For these, you can't really use a Gamma or a log-Normal.

In the paper, I extend the framework of hurdle models commonly used to tackle the issue of individual patients with observed zero costs, to include a full cost-effectiveness model, accounting for correlation between costs and a suitable measure of clinical effectiveness (eg QALYs). Basically, I do this using a structure consisting of:

1. a selection model for the chance of observing a zero cost, typically as a function of some individual covariates (eg age and sex);
2. a marginal model for the costs, inducing a mixture (of subjects with 0 cost and subjects with positive costs), depending on the selection model;
3. a conditional model for the benefits, depending on the costs (so that correlation between $e,c$ is guaranteed).

In graphical terms, something like this.

The green part is the selection model, estimating the overall average probability of a zero cost, which is used to weigh the components of the mixture model (in red). The observed costs have a distribution which is characterised by two parameters ($\eta$ and $\lambda$). These are modelled so that they induce a mean and variance of 0 for those subjects for whom the observed value is 0, and a proper (Gamma or log-Normal) distribution for the others. Finally, the blue part is the model for the benefits, which is defined as a (possibly generalised) linear regression, depending on the costs. The parameters $(\mu_c,\mu_e)$ are then used to do the cost-effectiveness analysis, eg using BCEA.

I've prepared a R package that would use this framework to do this analysis. I'm allowing for some possible distributions for both $c$ (Gamma and log-Normal) and $e$ (Beta, Bernoulli, Gamma and Normal). The package (which I'm provisionally calling BCES0, for Bayesian Cost-Effectiveness for Structural 0s) lets you select the distributional assumptions and then builds a model code and runs it in JAGS. The user doesn't even know how to code JAGS models (provided they're happy with the relative general model that will be produced automatically). But I'm making R save the model file, so that you can actually see it and modify it as needed. 

I'll post more once I've debugged the package and prepared a couple of nice examples (I'll put a working paper in here soon). I'll also give a talk on this at the LSHTM in the autumn $-$ more on this later!

Day out in Bristol (2)

PS (to the previous post): [I'm assuming] during a break from taking care of her own XX, Silvia points out that the graffiti in the picture here is nothing less than an original Bansky, pretty much as this one, which I see every morning on my way to work...

Day out in Bristol

Long day, today, as I went to Bristol for a workshop on the expected value of information, specifically for health economic evaluation.

I like Bristol $-$ I've only been a couple of times, really, but it feels like a fun place (as suggested by the awesome graffiti on a wall close to the station)...

The workshop was presented by Nicky Welton, Marta Soares and Tony Ades (actually, Nicky did most of the talks). I enjoyed the day, although I would have liked more technical sessions $-$ not criticising here: I think the intention was to give a general introduction to the concepts underpinning the EVPI and other derived indicators, such as the expected value of parameter information and the the expected value of sample information. 

In this sense, the workshop was well designed. But I wouldn't have minded more details both on the methods and the computational aspects, especially as some of the example presented looked based on relatively complex models, which would have been nice to learn more about.

Plan B

Thank goodness, I think that even if this statistician business turns out badly, I can still make a living with rafting (if only by begging for money, in exchange for looking ridiculous in the swim suit)... 

As part as my brother's stag do, we went to the Cascata delle Marmore and gave it a go. It was good fun. First we spent a good 45 minutes being briefed and taught the theory. 

The guy who was doing this was a bit of a drama queen and made it out much worse and dangerous than it actually is... 
Our team did well, although we were told off several times by the instructor. 

Back home and to a gazillion emails. And tomorrow I'll be in Bristol to a Workshop on the Value of Information, organised by the ConDuCT Hub for Trials Methodology Research, University of Bristol. It promises to be quite interesting. There'll be talks and case studies (for which I still haven't really done the suggested homework $-$ hopefully I'll manage to stay awake on the train to Bristol!).

On a different (but vaguely related) note, the updated version of BCEA is now available from CRAN (I've discussed the main changes here). The new manual is available here.